Temporal correlation function of Kelvin wave amplitudes at finite temperatures
Abstract
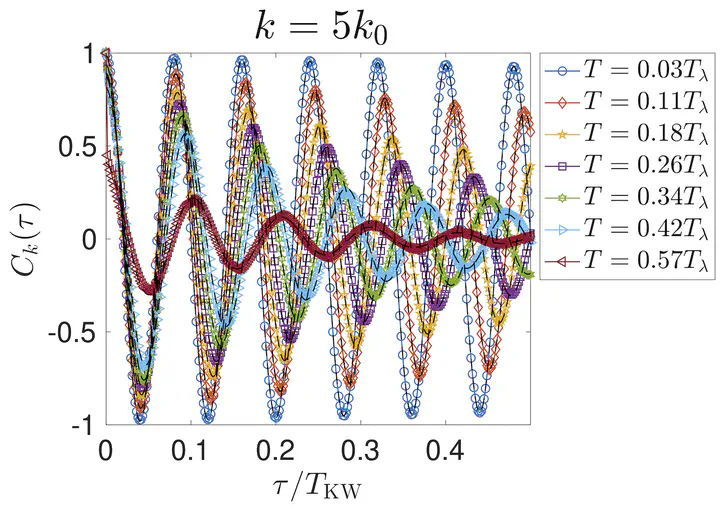
In this work we first briefly review some of the mutual friction effects on vortex lines and rings that were obtained in the context of the truncated Gross-Pitaevskii equation in references Krstulovic & Brachet [Phys. Rev. E 83(6), 066311 and Phys.Rev.B 83, 132506 (2011)], with particular attention to the anomalous slowdown of rings produced by thermally excited Kelvin waves. We then study the effect of mutual friction on the relaxation and fluctuations of Kelvin waves on straight vortex lines by comparing the results of full 3D direct simulations of the truncated Gross-Pitaevskii equation with a simple stochastic Local-Induction-Approximation model with mutual friction and thermal noise included. This new model allows us to determine the mutual friction coefficient α and α′ for the truncated Gross-Pitaevskii equation.