Self-similar evolution of the wave action spectra in inverse and direct cascade propagation.
Abstract
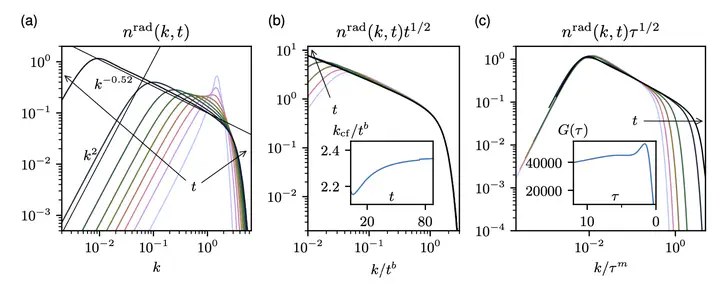
We study the universal nonstationary evolution of wave turbulence (WT) in Bose-Einstein condensates (BECs). Their temporal evolution can exhibit different kinds of self-similar behavior corresponding to a large-time asymptotic of the system or to a finite-time blowup. We identify self-similar regimes in BECs by numerically simulating the forced and unforced Gross-Pitaevskii equation (GPE) and the associated wave kinetic equation (WKE) for the direct and inverse cascades, respectively. In both the GPE and the WKE simulations for the direct cascade, we observe the first-kind self-similarity that is fully determined by energy conservation. For the inverse cascade evolution, we verify the existence of a self-similar evolution of the second kind describing self-accelerating dynamics of the spectrum leading to blowup at the zero mode (condensate) at a finite time. We believe that the universal self-similar spectra found in the present paper are as important and relevant for understanding the BEC turbulence in past and future experiments as the commonly studied stationary Kolmogorov-Zakharov (KZ) spectra