Turbulence and far-from-equilibrium equation of state of Bogoliubov waves in Bose-Einstein Condensates
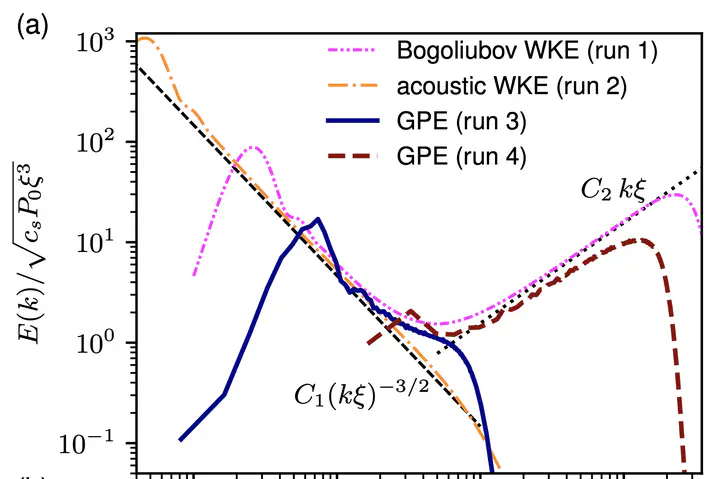 Energy spectrum of Bogoliubov wave turbulence
Energy spectrum of Bogoliubov wave turbulence
Abstract
Bogoliubov waves emerge when the system is perturbed from its ground state in a Bose-Einstein Condensate (BEC). These waves can interact nonlinearly, leading to turbulent cascades. In the present work, the turbulence of random weakly nonlinear Bogoliubov waves on the background of a uniform condensate is considered theoretically, within the Wave Turbulence approach, and numerically, via numerical simulations of the 3-dimensional (3D) Gross-Pitaevskii model and the associated wave-kinetic equations. A new Kolmogorov-like stationary spectrum is found for the short Bogoliubov waves. An exact prefactor constant was found for the previously known Zakharov-Sagdeev spectrum of long (acoustic) Bogoliubov waves. The results are used to explain the BEC equation of state experimentally obtained in [Dora et al. Nature 620,521 (2023)], and to suggest new settings for future experiments.