Abstract
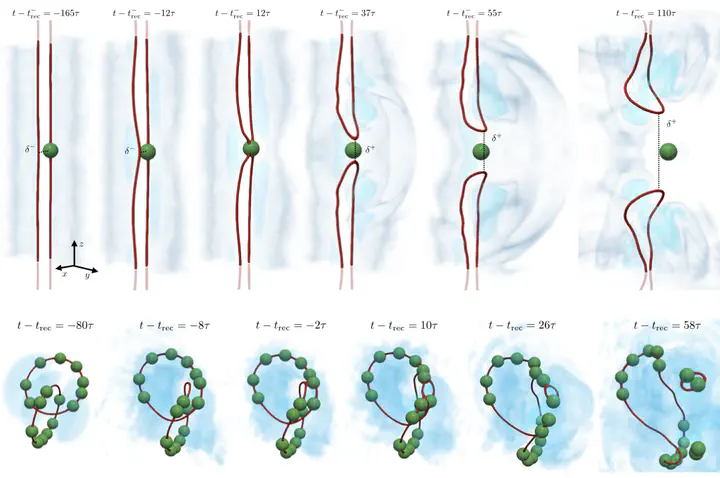
Reconnections between quantum vortex filaments in presence of trapped particles are investigated using numerical simulations of the Gross–Pitaevskii equation. Particles are described with classical degrees of freedom and modeled as highly repulsive potentials which deplete the superfluid. First, the case of a vortex dipole with a single particle trapped inside one of the vortices is studied. It is shown that the reconnection takes place at the position of the particle as a consequence of the symmetry breaking induced by it. The separation rate between the reconnecting points is compatible with the known dynamics of quantum vortex reconnections and it is independent of the particle mass and size. After the reconnection, the particle is pushed away with a constant velocity and its trajectory is deflected because of the transverse momentum exchange with the vortex filaments. The momentum exchanges between the particle, the vortex, and a density pulse are characterized. Finally, the reconnection of two linked rings, each of them with several initially randomly distributed particles is studied. It is observed that generically, reconnections take place at the location of trapped particles. It is shown that reconnection dynamics is unaffected for light particles.
Particles are today the main experimental tool to visualise quantum vortex dynamics. In particular, they have been used to study quantum vortex reconnections. The figure above shows numerical simulations of the Gross-Pitaevskii model, where vortices with trapped particles reconnect.