Velocity Circulation Intermittency in Finite-Temperature Turbulent Superfluid Helium

Abstract

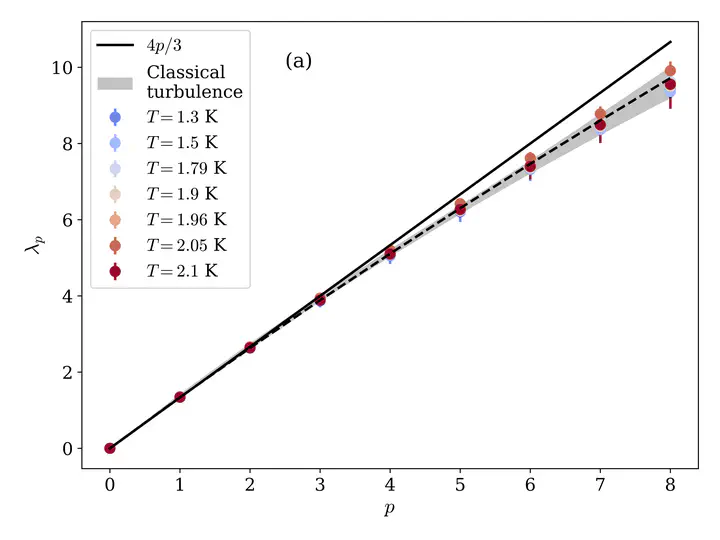
We study intermittency of circulation moments in turbulent superfluid helium by using experimental grid turbulence and numerical simulations of the Hall-Vinen-Bekarevich-Khalatnikov model. More precisely, we compute the velocity circulation $Γ_r$ in loops of size $r$ laying in the inertial range. For both, experimental and numerical data, the circulation variance shows a clear Kolmogorov scaling $<Γ^2_r>∼r^{8/3}$ in the inertial range, independently of the temperature. Scaling exponents of high-order moments are comparable, within error bars, to previously reported anomalous circulation exponents in classical turbulence and low-temperature quantum turbulence numerical simulations.