Exploring the Equivalence between Two-Dimensional Classical and Quantum Turbulence through Velocity Circulation Statistics
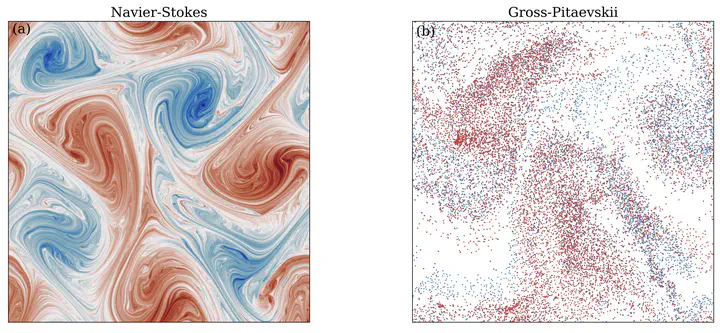 Vorticity in the enstrophy cascade in classical (left) and quantum (right) turbulence
Vorticity in the enstrophy cascade in classical (left) and quantum (right) turbulence
Abstract
We study the statistics of velocity circulation in two-dimensional classical and quantum turbulence. We perform numerical simulations of the incompressible Navier-Stokes and the Gross-Pitaevskii (GP) equations for the direct and inverse cascades. Our GP simulations display clear energy spectra compatible with the double cascade theory of two-dimensional classical turbulence. In the inverse cascade, we found that circulation intermittency in quantum turbulence is the same as in classical turbulence. We compare GP data to Navier-Stokes simulations and experimental data from [Zhu et al. Phys. Rev. Lett. 130, 214001(2023)]. In the direct cascade, for nearly incompressible GP-flows, classical and quantum turbulence circulation displays the same self-similar scaling. When compressible effects become important, quasi-shocks generate quantum vortices and the equivalence of quantum and classical turbulence only holds for low-order moments. Our results establish the boundaries of the equivalence between two-dimensional classical and quantum turbulence.