 Quantum (wave) turbulence in a trapped BEC
Quantum (wave) turbulence in a trapped BEC
Abstract
When a Bose-Einstein condensate (BEC) is driven out of equilibrium, density waves interact non-linearly and trigger the emergence of turbulent cascades. In a turbulent BEC, energy is transferred towards small scales by a direct cascade, whereas the number of particles displays an inverse cascade toward large scales. In this work, we study analytically and numerically the direct and inverse cascades in wave-turbulent BECs. We analytically derive the Kolmogorov-Zakharov spectra, including the universal pre-factor constants and the log-correction to the direct cascade scaling. We test and corroborate our predictions using high-resolution numerical simulations of the forced-dissipated Gross-Pitaevskii model in a periodic box and the corresponding wave-kinetic equation. Theoretical predictions and data are in excellent agreement, without adjustable parameters. Moreover, in order to connect with experiments, we successfully test our theoretical predictions using the Gross-Pitaevskii model with a cubic trap. Our results explain previous experimental observations and suggest new experimental settings for future studies.
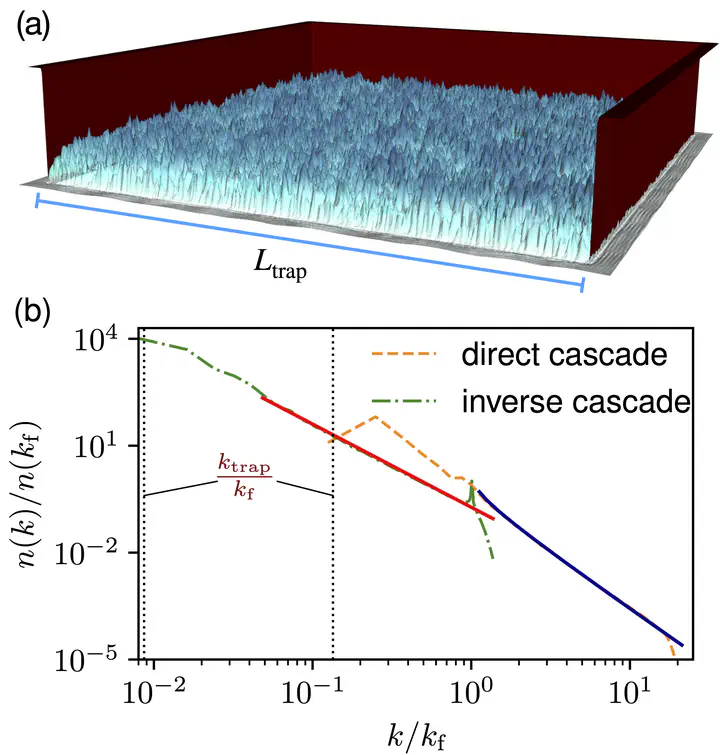
The figure above show the results of Gross-Pitaevskii simulations of a three-dimensional turbulent BEC. In (a) we see an snapshot of the turbulent BEC and the trap that confines it. Figure (b) show the wave-action spectrum (occupation number) in the inverse and direct cascades settings. The dashed lines display our theoretical predictions without any adjustable parameter.