Umberto Giuriato PhD Thesis

Dynamics of active particles in superfluids and their interaction with quantum vortices

Université Côte d’Azur. November 20th 2020.

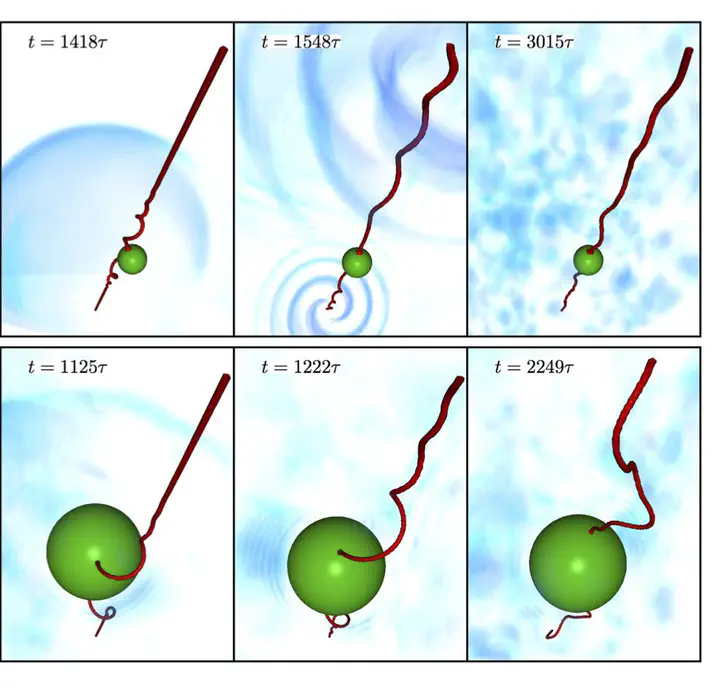
Superfluids are inviscid flows in which vorticity is supported on filaments with quantized circulation. Such objects, known as quantum vortices, exhibit a hydrodynamical behavior. Experimentally, the dynamics of superfluids has been studied by using particles, which nowadays have become the main tool for visualizing quantum vortices. In this Thesis, we study numerically and analytically the dynamics of active and finite-size particles in superfluids. The superfluid is modeled with the Gross– Pitaevskii equation, while the particles are implemented as moving repulsive potentials coupled with the macroscopic wave function describing the superfluid. Firstly, the model is used to investigate the interaction between particles and quantum vortices at very low temperatures. This part aims to give a theoretical background to the current experiments in which macroscopic particles are used to sample superfluid vortices and quantum turbulence. Specifically, we address the following problems: the capture of a particle by a quantum vortex, the reconnections of vortex filaments and the propagation of Kelvin waves in presence trapped particles and the dynamics of particles in decaying quantum turbulence. In the last part of the manuscript, finite temperature effects are studied in the Fourier-truncated Gross– Pitaevskii model. The goal is to characterize the dynamics of impurities immersed in a thermal bath and how their presence modifies the statistical properties of the fluid. In particular, the random motion of the impurities and the temperature dependence of the friction coefficient are studied. Finally, the clustering of impurities and its effect on the phase transitions of the condensate are investigated.