Energy Spectrum of Two-Dimensional Acoustic Turbulence
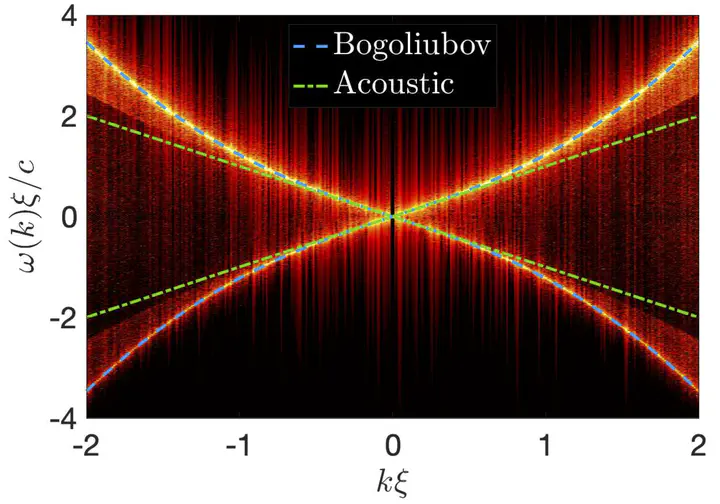 Dispersion relation of a weakly dispersive acoustic turbulence
Dispersion relation of a weakly dispersive acoustic turbulence
Abstract
We report an exact unique constant-flux power-law analytical solution of the wave kinetic equation for the turbulent energy spectrum, E(k)=C1 (εac)^{1/2}/k, of acoustic waves in 2D with almost linear dispersion law, ωk=ck[1+(ak)2], ak≪1. Here ε is the energy flux over scales, and C1 is the universal constant which was found analytically. Our theory describes, for example, acoustic turbulence in 2D Bose-Einstein condensates (BECs). The corresponding 3D counterpart of turbulent acoustic spectrum was found over half a century ago, however, due to the singularity in 2D, no solution has been obtained until now. We show the spectrum E(k) is realizable in direct numerical simulations of forced-dissipated Gross-Pitaevskii equation in the presence of strong condensate.